Integral Tertentu untuk Menghitung Luas Daerah

Luas Daerah yang Dibatasi oleh Kurva dengan Sumbu X

Luas daerah yang dibatasi oleh kurva $y = f\left( x \right)$ sumbu $X$, garis $x = a$, dan garis $x = b$ ditentukan oleh:

• $L = \int\limits_a^b {f\left( x \right)} dx,\text{untuk }f\left( x \right) \ge 0$
• $L = - \int\limits_a^b {f\left( x \right)} dx,\text{untuk }f\left( x \right) \le 0$

Luas Daerah yang Dibatasi oleh Beberapa Kurva

Luas daerah yang dibatasi oleh kurva $y = f\left( x \right)$, $y = g\left( x \right)$, garis $x = a$, dan $x = b$ ditentukan dengan rumus:

\[L = \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\]

Dengan catatan $f\left( x \right) \ge g\left( x \right)$ dalam interval tertutup $a \le x \le b$.

Contoh Soal

Hitunglah luas daerah yang dibatasi oleh kurva-kurva berikut dengan menggunakan integral tertentu

1. Luas daerah yang dibatasi oleh kurva $y=2x$, sumbu $X$, garis $x=1$, dan $x=3$.
2. Luas daerah yang dibatasi oleh kurva $y = {x^2} + 2$, sumbu $X$, garis $x=-1$, dan $x=2$.
3. Luas daerah yang dibatasi oleh kurva $y = - x$ dan $y = {x^2} + 2x$.
4. luas daerah yang dibatasi oleh kurva $y = {x^2}$ dan $y = {x^3}$.

Jawab

1. Luas daerah yang dibatasi oleh kurva $y=2x$, sumbu $X$, garis $x=1$, dan $x=3$.

Perhatikan grafik berikut:



Dari grafik di atas, pada interval $1 \le x \le 3$ grafik fungsi $y=2x$ berada di atas sumbu $X$. Luas daerahnya dapat dihitung sebagai berikut:

$\begin{array}{l} L &= \int\limits_1^3 {f\left( x \right)} dx\\ &= \int\limits_1^3 {2x} dx\\ &= \left[ {{x^2}} \right]_1^3\\ &= \left( {{3^2}} \right) - \left( {{1^2}} \right)\\ &= 9 - 1\\ &= 8 \end{array}$

Jadi, luas daerah yang dibatasi oleh kurva $y=2x$, sumbu $X$, garis $x=1$, dan $x=3$ adalah $8$ satuan luas.

2. Luas daerah yang dibatasi oleh kurva $y = {x^2} + 2$, sumbu $X$, garis $x=-1$, dan $x=2$.

Perhatikan grafik berikut:



Dari grafik di atas, pada interval $-1 \le x \le 2$ grafik fungsi $y = {x^2} + 2$ berada di atas sumbu $X$. Luas daerahnya dapat dihitung sebagai berikut:

$\begin{array}{l} L &= \int\limits_{ - 1}^2 {f\left( x \right)} dx\\ &= \int\limits_{ - 1}^2 {\left( {{x^2} + 2} \right)} dx\\ &= \left[ {\frac{1}{3}{x^3} + 2x} \right]_{ - 1}^2\\ &= \left( {\frac{1}{3}{2^3} + 2.2} \right) - \left( {\frac{1}{3}{{\left( { - 1} \right)}^3} + 2.\left( { - 1} \right)} \right)\\ &= \left( {\frac{8}{3} + 4} \right) - \left( { - \frac{1}{3} - 2} \right)\\ &= \frac{8}{3} + 4 + \frac{1}{3} + 2\\ &= 9 \end{array}$

Jadi, luas daerah yang dibatasi oleh kurva $y = {x^2} + 2$, sumbu $X$, garis $x=-1$, dan $x=2$ adalah $9$ satuan luas.

3. Luas daerah yang dibatasi oleh kurva $y = - x$ dan $y = {x^2} + 2x$.

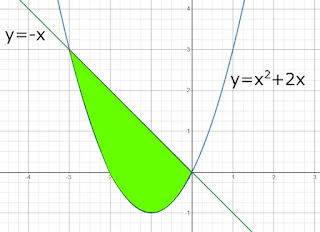
Perhatikan grafik berikut:



Dari grafik di atas misalkan $f\left( x \right) = y = - x$ dan $g\left( x \right) = y = {x^2} + 2x$ maka $f\left( x \right) \ge g\left( x \right)$ pada daerah yang di arsir. Untuk menentukan batas atas dan batas bawah pengintegralan dapat dicari dengan cara berikut:

$\begin{array}{l} f\left( x \right) &= g\left( x \right)\\ \Leftrightarrow - x &= {x^2} + 2x\\ \Leftrightarrow {x^2} + 2x &= - x\\ \Leftrightarrow {x^2} + 2x + x &= 0\\ \Leftrightarrow {x^2} + 3x &= 0\\ \Leftrightarrow x\left( {x + 3} \right) &= 0\\ x = 0 \vee x + 3 = 0\\ x = 0 \vee x = - 3 \end{array}$

Diperoleh batas bawah $x = - 3$ dan batas atas $x = 0$. Luas daerahnya dapat dihitung sebagai berikut:

$\begin{array}{l} L &= \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\\ &= \int\limits_{ - 3}^0 {\left[ {\left( { - x} \right) - \left( {{x^2} + 2x} \right)} \right]} dx\\ &= \int\limits_{ - 3}^0 {\left[ { - x - {x^2} - 3x} \right]} dx\\ &= \int\limits_{ - 3}^0 {\left[ { - {x^2} - 4x} \right]} dx\\ &= \left[ { - \frac{1}{3}{x^3} - 2{x^2}} \right]_{ - 3}^0\\ &= \left( { - \frac{1}{3}{{.0}^3} - {{2.0}^2}} \right) - \left( { - \frac{1}{3}{{\left( { - 3} \right)}^3} - 2{{\left( { - 3} \right)}^2}} \right)\\ &= 0 - \left( { - \frac{1}{3}\left( { - 27} \right) - 2.9} \right)\\ &= 0 - \left( {9 - 18} \right)\\ &= 9 \end{array}$

Jadi, luas daerah yang dibatasi oleh kurva $y = - x$ dan $y = {x^2} + 2x$ adalah $9$ satuan luas.

4. Luas daerah yang dibatasi oleh kurva $y = {x^2}$ dan $y = {x^3}$.

Perhatikan grafik berikut:



Dari grafik di atas misalkan $f\left( x \right) = y = {x^2}$ dan $g\left( x \right) = y = {x^3}$ maka $f\left( x \right) \ge g\left( x \right)$ pada daerah yang di arsir. Untuk menentukan batas atas dan batas bawah pengintegralan dapat dicari dengan cara berikut:

$\begin{array}{l} f\left( x \right) &= g\left( x \right)\\ \Leftrightarrow {x^2} &= {x^3}\\ \Leftrightarrow {x^2} - {x^3} &= 0\\ \Leftrightarrow {x^2}\left( {1 - x} \right) &= 0\\ \Leftrightarrow {x^2} = 0 \vee 1 - x = 0\\ \Leftrightarrow x = 0 \vee x = 1 \end{array}$

Diperoleh batas bawah $x = 0$ dan batas atas $x = 1$. Luas daerahnya dapat dihitung sebagai berikut:

$\begin{array}{l} L &= \int\limits_0^1 {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\\ &= \int\limits_0^1 {\left[ {{x^2} - {x^3}} \right]} dx\\ &= \left[ {\frac{1}{3}{x^3} - \frac{1}{4}{x^4}} \right]_0^1\\ &= \left( {\frac{1}{3}{{.1}^3} - \frac{1}{4}{{.1}^4}} \right) - \left( {\frac{1}{3}{{.0}^3} - \frac{1}{4}{{.0}^4}} \right)\\ &= \left( {\frac{1}{3} - \frac{1}{4}} \right) - 0\\ &= \frac{1}{{12}} \end{array}$

Jadi, luas daerah yang dibatasi oleh kurva $y = {x^2}$ dan $y = {x^3}$ adalah $\frac{1}{{12}}$ satuan luas.